Beneficial Ownership Visualisation System
Summarisation of Interests
You may wish to summarise the interests of more than one Party as a single figure. For instance, to summarise the ownership interests of multiple Persons, or to give the ultimate result of a Chain of control interests.
Summarised figures might appear in the captions to your diagram, in its supporting text, or as part of the diagram itself through Optional Features such as Indirect Arrows or Charts.
Summarisation results in a quantified interest, that is, a percentage figure, even if the interests that were summarised were obscured or not quantified. However, the summarised figure may contain uncertainty (that is, it may be a range, e.g. 10-20%).
These summarised figures must obviously be mathematically accurate. This can be tricky to calculate when interests are obscured. Take care to follow the arithmetic rules below to ensure summarised figures are correct.
Overview
In general, interests are summarised in the following way:
- To combine interests of multiple Parties in a single Entity, use addition.
- To give the compounded interest of one Party, via intermediaries, in another, use multiplication.
Summarisation must focus on interests of a single nature, i.e. either ownership or control. In the below, we write just “interest” for brevity; this should be taken to mean “interest of the selected nature”.
Combined Interests (Addition)
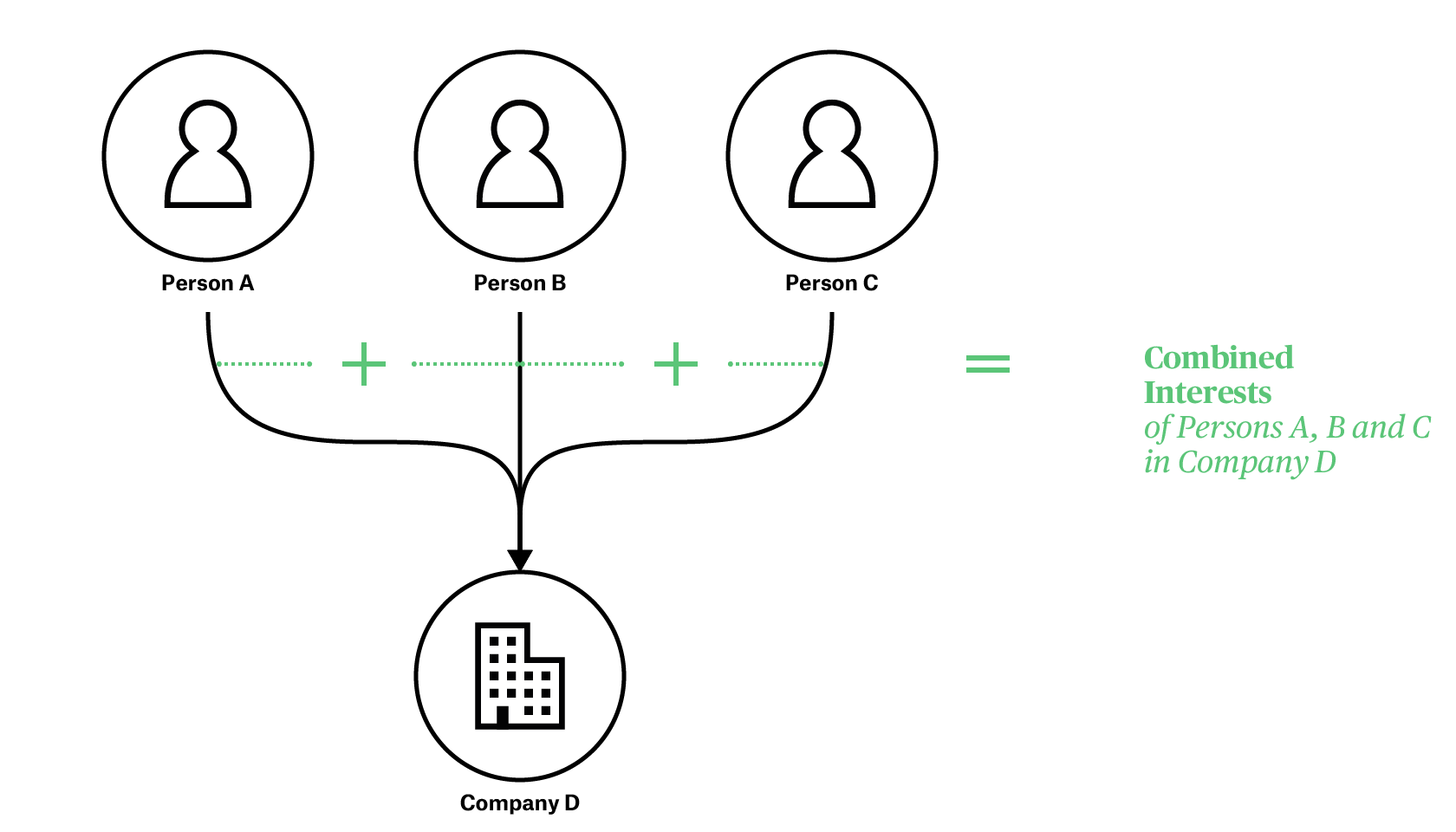
You may summarise the interests of multiple Parties in a given Entity by adding together each of their direct interests in that Entity. The summarised figure is referred to as their combined interest in the given Entity.
- Any Party that does not have a direct interest in the selected Entity is treated as a zero in the addition.
- See below for how to handle addition in cases where interests are obscured.
Uncertain Interests
If any interest in your addition is uncertain, i.e. is given as a range, then your output will also be uncertain. To calculate the result:
- Split all of your figures into a known and unknown portion.
- Add up the known and unknown portions separately.
- Recombine the known and unknown portions into a range.
| Party | Interest | Known Portion | Unknown Portion | |
|---|---|---|---|---|
| Person A | 10% | 10% | 0% | |
| Person B | + | 5-10% | 5% | 5% |
| Person C | + | 10-15% | 10% | 5% |
| Combined | = | 25-35% | 25% | 10% |
Addition involving uncertainty may result in a range with more than 100% as its upperbound. For instance:
| Party | Interest | Known Portion | Unknown Portion | |
|---|---|---|---|---|
| Person A | 50-75% | 50% | 25% | |
| Person B | + | 25-50% | 25% | 25% |
| Combined | = | 75-125% | 75% | 50% |
This accurately reflects our lack of knowledge about where these uncertainties overlap. That is, we don’t know whether the 25% unknown portion of Person A’s interest is completely accounted for by the 25% unknown portion of Person B’s interest.
Unknown Interests
If any interest in your addition is unknown, i.e. the nature or the strength of interest is not known:
- Treat this interest as a range from 0-100%.
- Follow the rules above for combining uncertain interests.
| Party | Interest | Known Portion | Unknown Portion | |
|---|---|---|---|---|
| Person A | Unknown Nature | 0% | 100% | |
| Person B | + | 10% | 10% | 0% |
| Combined | = | 10-110% | 10% | 100% |
| Party | Interest | Known Portion | Unknown Portion | |
|---|---|---|---|---|
| Person A | + | Unknown Strength | 0% | 100% |
| Person B | + | Unknown Nature | 0% | 100% |
| Person C | + | Unknown Strength | 0% | 100% |
| Combined | = | 0-300% | 0% | 300% |
Any result that is a range from 0% to 100% or more, i.e. a complete unknown, can be abbreviated as “?%”.
Unquantifiable Interests
If any interest in your addition includes an unquantifiable property, i.e. something that cannot be expressed as a figure:
- Split all of your figures into their quantifiable and unquantifiable parts.
- Ignore the unquantifiable parts for the purposes of the addition.
- Use your subjective assessment to determine if the result should include the unquantifiable parts (and which).
| Party | Interest | Quantifiable | Unquantifiable | |
|---|---|---|---|---|
| Person A | 5% | 5% | ||
| Person B | + | Influence | 0% | Influence |
| Person C | + | 5% | 5% | |
| Combined | = | 10% | 10% | |
| or | = | 10% + Influence | 10% | Influence |
When giving the combined control interests of the above 3 people, you might choose to give this as:
- “10%”, i.e. just the quantifiable result.
- “10% + Influence”, i.e. you feel that Person B is so influential that this should be noted even when she is grouped with 2 other Persons.
Compounded Interests (Multiplication)
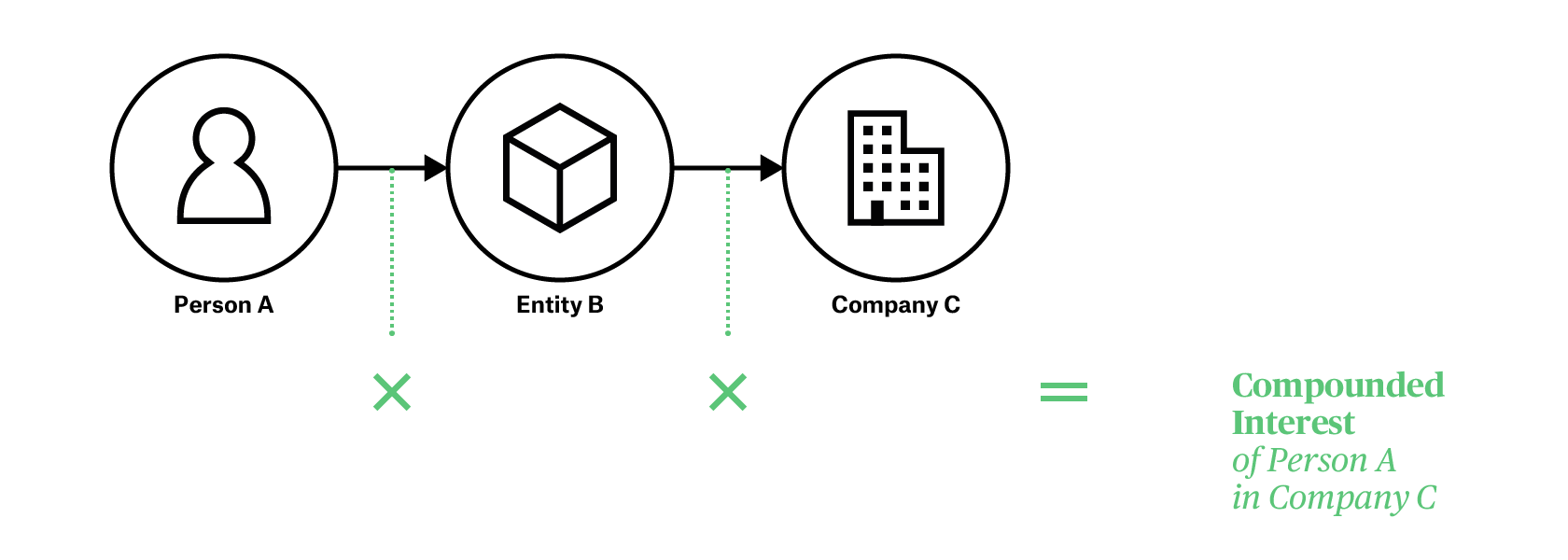
You may summarise the interest of a single Party in a distant Entity by multiplying together each direct interest along the Chain from the first Party to the final Entity. The summarised figure is referred to as the Party’s compounded interest in the given Entity.
- Any Party in the Chain that does not have a direct interest in the next Entity is treated as a zero in the multiplication.
- See below for how to handle multiplication in cases where interests are obscured.
Uncertain Interests
If any interest in your multiplication is uncertain, i.e. is given as a range, then your output will also be uncertain. To calculate the result:
- Split all of your figures into a lowerbound and upperbound.
- Multiply the lowerbounds and upperbounds separately.
- Recombine the lowerbounds and upperbounds into a range.
| Party | Interest | Lowerbound | Upperbound | |
|---|---|---|---|---|
| Entity A | 50% | 50% | 50% | |
| Entity B | × | 30-40% | 30% | 40% |
| Compounded | = | 15-20% | 15% | 20% |
| Party | Interest | Lowerbound | Upperbound | |
|---|---|---|---|---|
| Entity A | 50-75% | 50% | 75% | |
| Entity B | × | 30-40% | 30% | 40% |
| Compounded | = | 15-30% | 15% | 30% |
Unknown Interests
If any interest in your multiplication is unknown, i.e. the nature or the strength of interest is not known:
- Treat this interest as a range from 0-100%.
- Follow the rules above for compounding uncertain interests.
| Party | Interest | Lowerbound | Upperbound | |
|---|---|---|---|---|
| Entity A | Unknown Nature | 0% | 100% | |
| Entity B | × | 50% | 50% | 50% |
| Compounded | = | 0-50% | 0% | 100% |
| Party | Interest | Lowerbound | Upperbound | |
|---|---|---|---|---|
| Entity A | Unknown Strength | 0% | 100% | |
| Entity B | × | Unknown Nature | 0% | 100% |
| Entity C | × | Unknown Strength | 0% | 100% |
| Compounded | = | 0-100% | 0% | 100% |
Any result that is a range from 0% to 100% or more, i.e. a complete unknown, can be abbreviated as “?%”.
Unquantifiable Interests
If any interest in your multiplication includes an unquantifiable property, i.e. something that cannot be expressed as a figure:
- Split all of your figures into their quantifiable and unquantifiable parts.
- Ignore the unquantifiable parts for the purposes of the multiplication.
- Use your subjective assessment to determine if the result should include the unquantifiable parts (and which).
| Party | Interest | Quantifiable | Unquantifiable | |
|---|---|---|---|---|
| Person A | Influence | 0% | Influence | |
| Entity B | × | 50% | 50% | |
| Entity C | × | 50% | 50% | |
| Compounded | = | 0% | 0% | |
| or | = | Influence | 0% | Influence |
When giving the compounded interest of Person A, you might choose to give this as:
- “0%”, i.e. no control interest, if you consider that Person A’s influence is not strong enough to exert any control through 2 intermediaries
- “Influence”, i.e. you note that Entity B has 25% control (via Entity C), and you consider Person A to have a strong influence over Entity B
Interests >100%
Diagrams should be faithful to the data they are drawn from, and that data may sometimes imply a strength of interest that is greater than 100% (in either its known or unknown part). This may be because:
- The data is taken from different points in time
- The data contains errors
- The data contains ranges rather than absolute values
In each of these cases, visualising that the data implies interests greater than 100% is informative, highlighting the need for further checks on the data, or for care to be taken in data interpretation. It’s another way in which the diagram shows what we don’t know about the situation.
For this reason, it’s not advisable to round interests down to 100%. However, if such manipulation is unavoidable for a particular use case, note within the diagram that you have done this, and provide a clear explanation of the process and rationale in your supporting text.